Simulates data from the Choice-Confidence (CHOCO) model. This model is useful for subjective ratings (e.g., Likert-type scales) where responses represent a choice between two underlying categories (e.g., "disagree" vs. "agree") along with a degree of confidence or intensity.
The CHOCO model divides the response scale at a middle-value. Responses above and below the
middle are modeled by two rescaled (and mirrored for the left side) Beta-Gate distributions.
In Beta-Gate distributions, extreme values (0 or 1) are generated by the "lumping" of values
that crossed a threshold (or "gate"). The location of these gates from the center of the
distribution is controlled by the pex and bex parameters, influecing the ease of crossing
the gate (and thus the probability of extreme values).
Usage
rchoco(
n,
p = 0.5,
confright = 0.5,
precright = 4,
confleft = 0.5,
precleft = 4,
pex = 0.1,
bex = 0.5,
pmid = 0,
mid = 0.5
)
dchoco(
x,
p = 0.5,
confright = 0.5,
precright = 4,
confleft = 0.5,
precleft = 4,
pex = 0.1,
bex = 0.5,
pmid = 0,
mid = 0.5,
log = FALSE
)
choco_lpdf_expose()
choco_stanvars()
choco(
link_mu = "logit",
link_confright = "logit",
link_precright = "softplus",
link_confleft = "logit",
link_precleft = "softplus",
link_pex = "logit",
link_bex = "logit",
link_pmid = "logit"
)
log_lik_choco(i, prep)
posterior_predict_choco(i, prep, ...)
posterior_epred_choco(prep)Arguments
- n
Number of simulated trials.
- p
Proportion parameter determining the balance between the left and right sides after excluding the probability mass at the middle (
pmid).P(Right Side | Not Middle) = p.- confright, confleft
Mean parameter (
mu) for the underlying Beta-Gate distribution for the right side and left side, respectively. Represents confidence towards 1.0 < confright < 1.- precright, precleft
Precision parameter (
phi) for the underlying Beta-Gate distribution for the right side and left side, respectively. Must be positive. Higher values indicate more concentrated distributions, and a value of 1 corresponds to a uniform distribution.- pex
Controls the location of the lower and upper boundary gates (
0 <= pex <= 1). It defines the total probability mass allocated to the extremes (0 or 1). Higherpexincreases the probability of extreme values (0 or 1).- bex
Balances the extreme probability mass
pexbetween 0 and 1 (0 <= bex <= 1). A balance of0.5means that the 'gates' are symmetrically placed around the center of the distribution, and values higher or lower than0.5will shift the relative "ease" of crossing the gates towards 1 or 0, respectively.- pmid
Probability mass exactly at the
mid. This determines the proportion of trials where the output is directly assigned the value ofmid, bypassing the left or right components.- mid
The point dividing the scale (
0 < mid < 1). Typically set to 0.5. Note that in the Stan implementation,midis fixed at 0.5 and not available as a parameter.- x
Vector of quantiles (values at which to evaluate the density). Must be between 0 and 1, inclusive.
- log
Logical; if TRUE, returns the log-density.
- link_mu, link_confright, link_precright, link_confleft, link_precleft, link_pex, link_bex, link_pmid
Link functions for the parameters.
- i, prep
For brms' functions to run: index of the observation and a
brmspreparation object.- ...
Additional arguments.
Details
Psychological Interpretation:
p: Represents the overall tendency to choose the "right" category (e.g., "agree") over the "left" category (e.g., "disagree"), given that a choice is made (i.e., not responding exactly atmid).confrightandconfleft: Average confidence level when choosing the "right" or "left" category. Higher values (closer to 1) indicate stronger confidence or agreement towards the extreme end of the scale.precrightandprecleft: Certainty or consistency of the confidence ratings for the right and left choices, respectively. Higher values indicate less variability in confidence ratings around their respective means (confright,confleft).pex: Represents the overall tendency towards extreme responding (choosing 0 or 1). This could reflect individual response styles (e.g., acquiescence, yea-saying/nay-saying) or properties of the item itself (e.g., polarizing questions).bex: Indicates the direction of the extreme response bias.bex > 0.5suggests a bias for producing ones more easily, whilebex < 0.5suggests a bias towards zero.
References
Kubinec, R. (2023). Ordered beta regression: a parsimonious, well-fitting model for continuous data with lower and upper bounds. Political Analysis, 31(4), 519-536. (Describes the underlying ordered beta model)
Examples
# Simulate data with different parameterizations
# 10% at mid, 50/50 split otherwise, symmetric confidence/precision
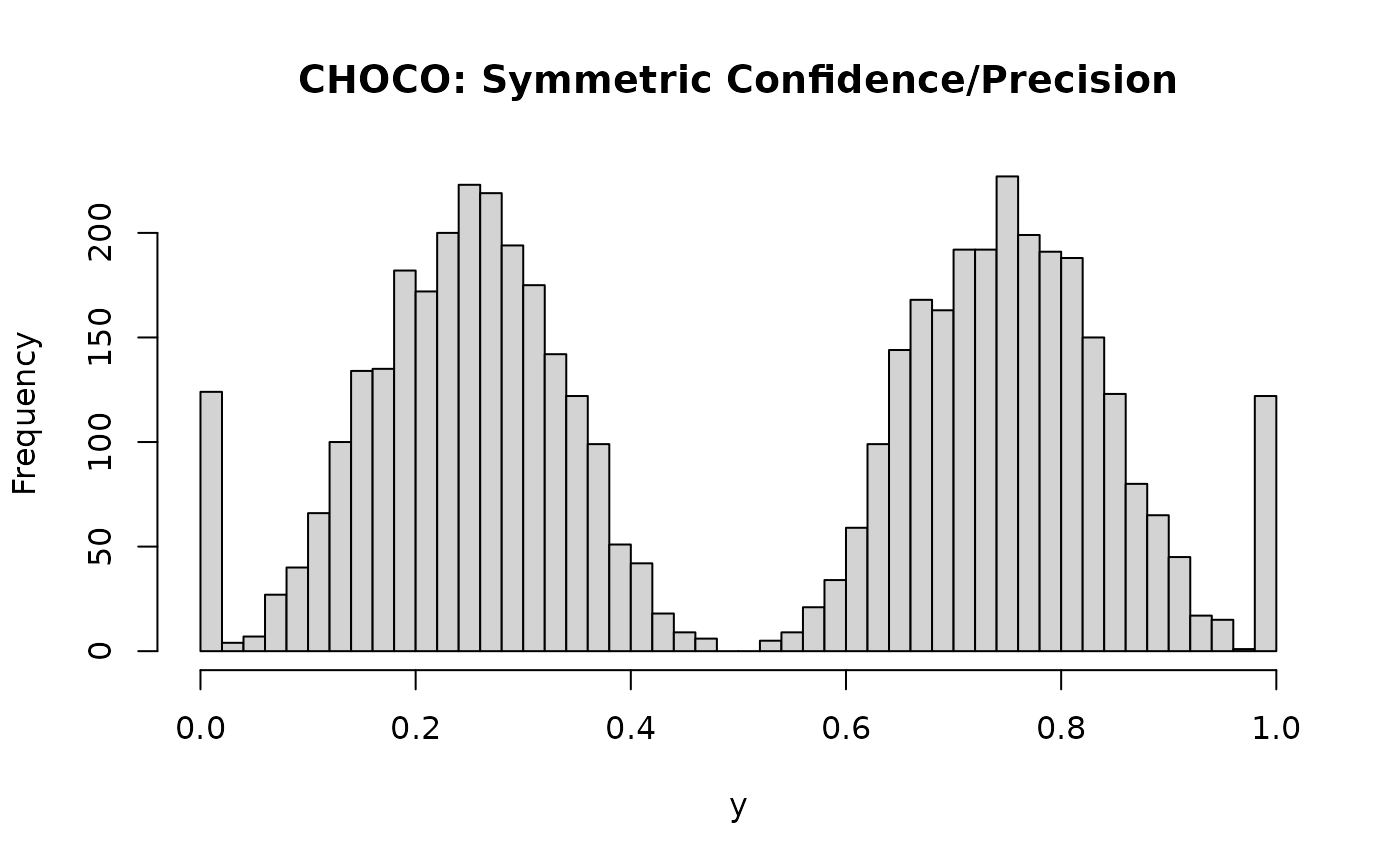
x1 <- rchoco(n=5000, p = 0.5, confright = 0.5, precright = 4,
confleft = 0.5, precleft = 4, pex = 0.1, bex = 0.5, pmid = 0, mid = 0.5)
hist(x1, breaks = 50, main = "CHOCO: Symmetric Confidence/Precision", xlab = "y")
 # No mid mass, 70% probability on right, higher confidence left (closer to 0)
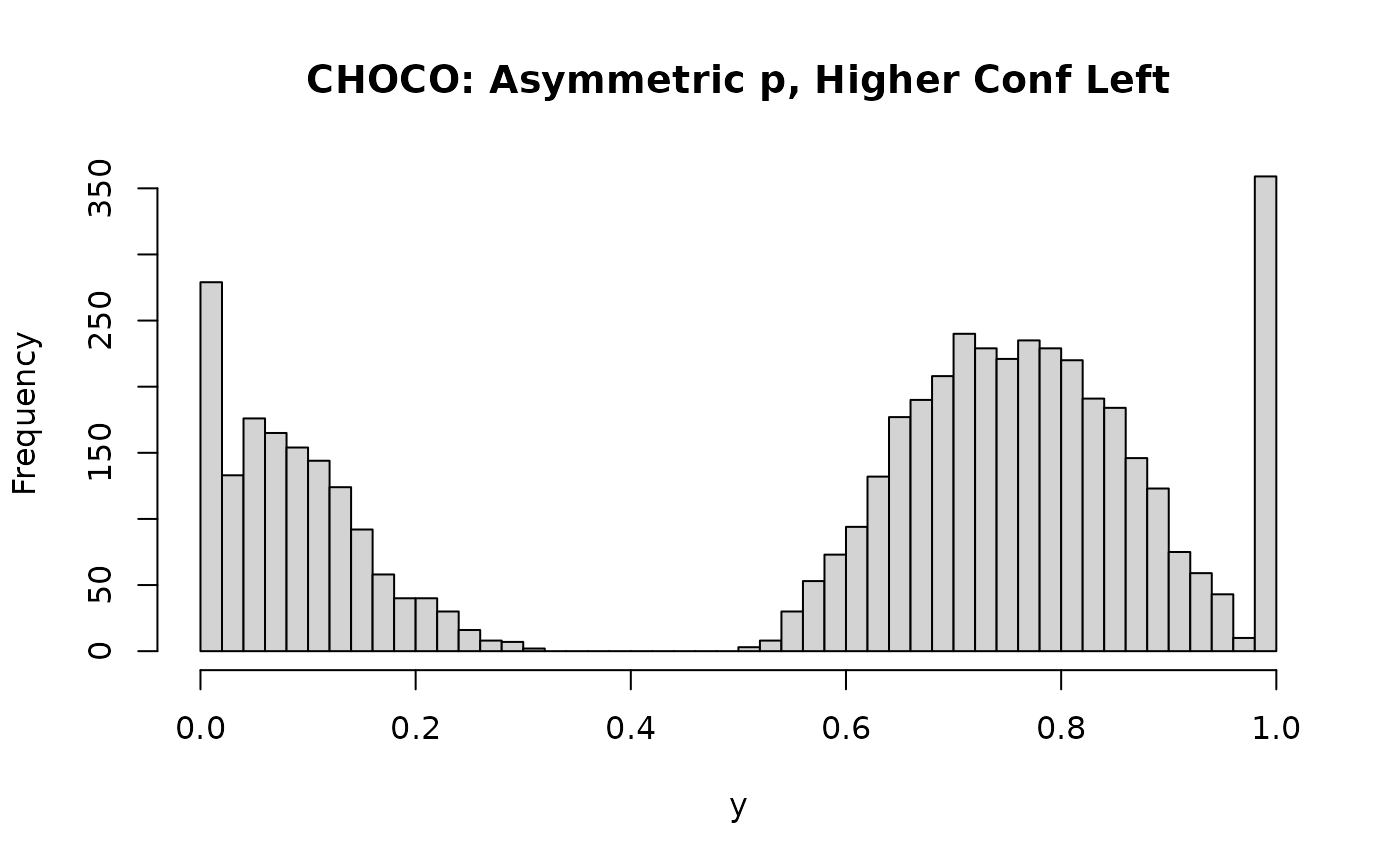
x2 <- rchoco(n=5000, p = 0.7, confright = 0.5, precright = 3,
confleft = 0.8, precleft = 5, pex = 0.15, bex = 0.7, pmid = 0, mid = 0.5)
hist(x2, breaks = 50, main = "CHOCO: Asymmetric p, Higher Conf Left", xlab = "y")
# No mid mass, 70% probability on right, higher confidence left (closer to 0)
x2 <- rchoco(n=5000, p = 0.7, confright = 0.5, precright = 3,
confleft = 0.8, precleft = 5, pex = 0.15, bex = 0.7, pmid = 0, mid = 0.5)
hist(x2, breaks = 50, main = "CHOCO: Asymmetric p, Higher Conf Left", xlab = "y")
 # Lower confidence overall (closer to mid), high probability in the middle
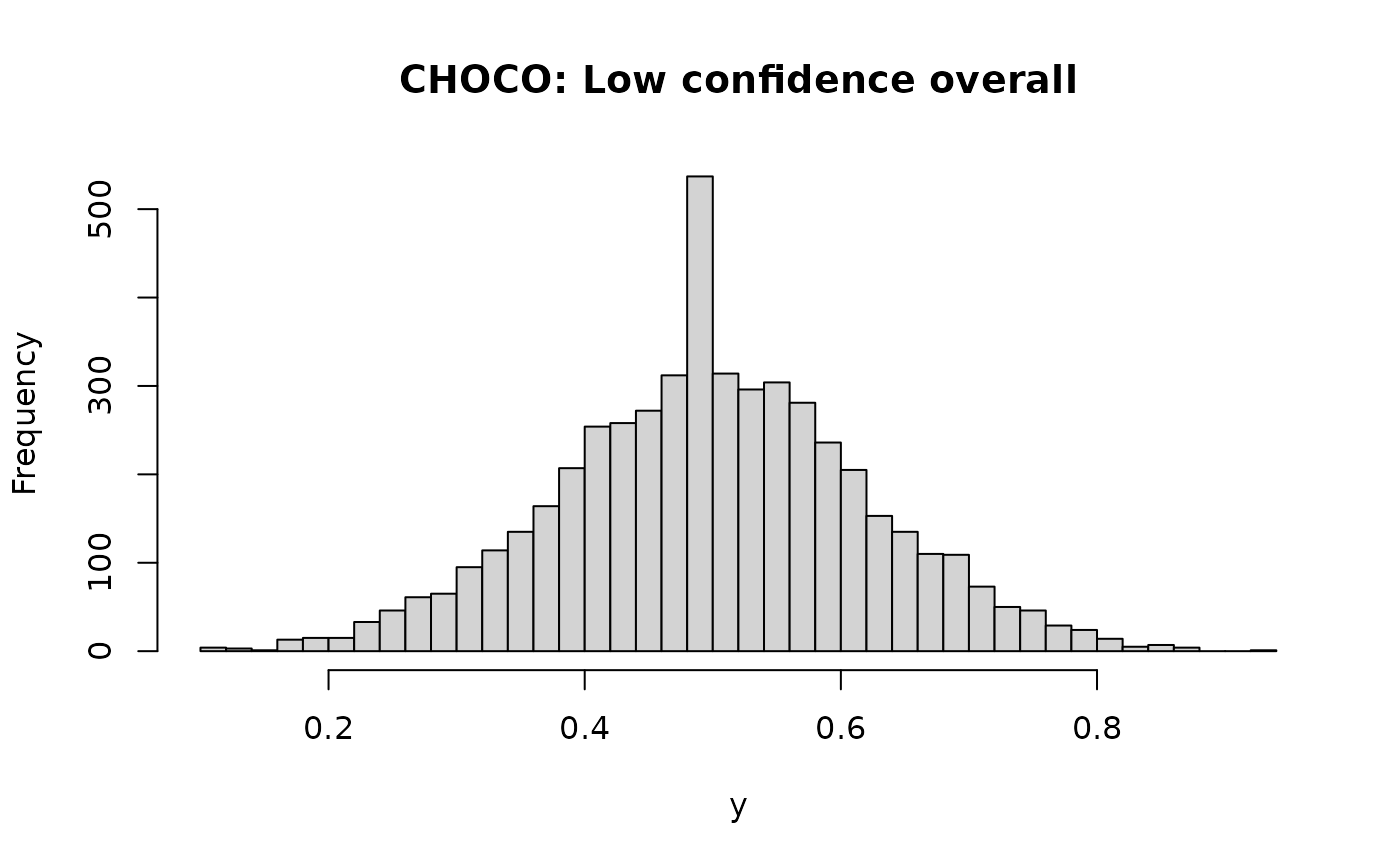
x3 <- rchoco(n=5000, p = 0.5, confright = 0.2, precright = 3,
confleft = 0.2, precleft = 3, pex = 0, bex = 0.5, pmid = 0.05, mid = 0.5)
hist(x3, breaks = 50, main = "CHOCO: Low confidence overall", xlab = "y")
# Lower confidence overall (closer to mid), high probability in the middle
x3 <- rchoco(n=5000, p = 0.5, confright = 0.2, precright = 3,
confleft = 0.2, precleft = 3, pex = 0, bex = 0.5, pmid = 0.05, mid = 0.5)
hist(x3, breaks = 50, main = "CHOCO: Low confidence overall", xlab = "y")
 if (FALSE) { # \dontrun{
# Example usage in brm formula:
# bf(y ~ x1 + (1|group),
# confright ~ x3,
# confleft ~ x3,
# precright ~ 1,
# precleft ~ 1,
# pex ~ s(age),
# bex ~ 1,
# pmid ~ 1,
# family = choco())
} # }
if (FALSE) { # \dontrun{
# Example usage in brm formula:
# bf(y ~ x1 + (1|group),
# confright ~ x3,
# confleft ~ x3,
# precright ~ 1,
# precleft ~ 1,
# pex ~ s(age),
# bex ~ 1,
# pmid ~ 1,
# family = choco())
} # }